New aspects of electrophylic aromatic substitution mechanism: Computational model of nitration reaction

Analysis of Substrates Reactivity

Thermochemical aspect

Because geometrical and electronic structure of TS1 and of σ-complex are similar, we expected existence of free energies linearity rule in that elementary reaction stage. This correlation is presented in Figure 6. (Negative values of some barriers was discussed above in the section titled “Gas Phase.”) The plot shows that points corresponding to ortho attack lie on the line situated below that of meta and para group. Evidently, this feature of ortho reaction can be explained by the appearance of steric interaction (to be precise, it appears in σ-complex and so increases its heat of formation). As to ipso attack, correlation is not very good, because of too great a steric effect. On the other hand, the same poor linearity was observed for relation of activation barriers and total enthalpy of nitration reaction. This can be explained by the absence of ring deformation contribution into the enthalpy of final nitro products.

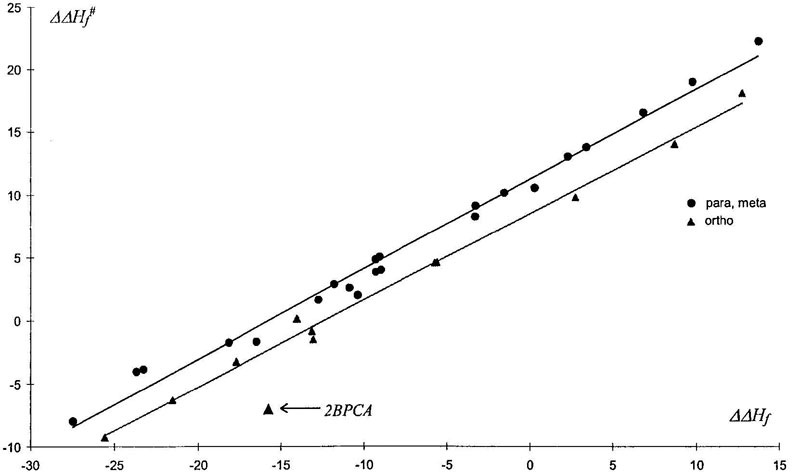Figure 6. Relation between activation barrier (ΔΔH^≠_f, kcal/mol) and enthalpy of σ-complex formation (ΔΔH_f, kcal/mol).

With regard to reactivity indexes, the only thermochemical parameter of reactivity is the enthalpy of σ-complex formation and not the total heat of reaction.

Another interesting case of ortho- effect was found in reaction with 2-biphenylcarbonic acid (2BPCA). Geometry of this molecule is such that in TS the carboxy group is turned by negatively charged oxygen atoms toward positive electrophil, which gives considerable gain to TS energy (2 kcal/mol for ortho attack and 1 kcal/mol for para)^*. Such additional interaction exists only in TS, for in σ-complex the total charge of nitrogroup is practically zero, and so it leads to deviation from linearity rule (see Fig. 6).

It is possible to compare calculated with reactivities observed in experiment. Attina and Cacace [13] measured rate constants of reaction of CH3O-NO2+ with alkyl and halogen benzenes in gas phase. Figure 7 shows that our calculations are in good agreement with observed reactivity of these compounds. Thermochemical calculations based on the SM2.1 method give analogous results: linear correlation between activation energy and enthalpy of σ-complex formation. Corresponding data are collected in Table VII.

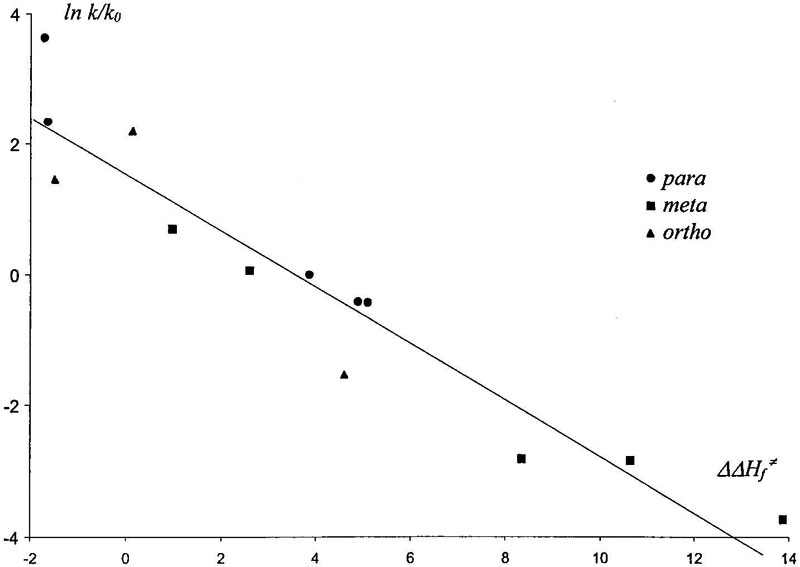Figure 7. Logarithmic plot of experimental reactivity versus calculated activation energies. Partial rate constants of gas-phase reaction of CH3O-NO2+ with methylbenzene, tret-butylbenzene, and Cl and F benzenes calculated relative to benzene rate constant from Ref. [13].

Table VII. Activation energy (ΔΔH^≠_f), enthalpy of σ-complex formation (ΔΔH^σ_f), total enthalpy of reaction (ΔΔH_f) relative to enthalpy of formation of isolated reagents, in kcal/mol, for reaction X-C6H5 + NO2+ ⇒ [X-C6H5-NO2]+ ⇒ X-C6H5-NO2 + H+.

X	ΔΔH≠f	ΔΔHσf	ΔΔHf
* σ-complex does not exist.
H	42.74	22.84	−71.74
CH3
para	40.67	20.48	−72.04
meta	43.28	24.06	−71.61
ortho	41.93	24.33	−69.71
ipso	46.03	35.56	—
Ph
para	41.64	21.46	−70.89
meta	44.22	25.62	−70.68
ortho	42.87	26.79	−66.47
ipso	50.45	38.22	—
OAc
para	41.83	21.59	−69.99
meta	46.49	28.71	−69.65
ortho	44.23	26.34	−68.39
ipso	53.86	46.23	—
Cl
para	44.50	25.29	−69.72
meta	46.63	28.48	−69.29
ortho	45.27	28.96	−64.64
ipso	52.46	40.03	—
F
para	42.76	23.00	−69.70
meta	47.36	29.40	−68.68
ortho	43.71	24.98	−68.86
COOH
para	49.81	*	−67.76
meta	46.55	28.64	−68.41
ortho	50.33	34.38	−63.65
ipso	56.18	47.19	—
NO2
para	54.44	*	−65.31
meta	51.11	*	−66.10
ortho	54.79	39.79	−62.15
Pyridine, meta	46.14	26.73	−69.68
Naphtalene
α	39.86	19.58	−67.12
β	42.13	22.45	−70.56
Mezitilene	40.77	21.84	−67.55
ipso	46.95	37.07	—
Hexamethylbenzene	41.72	26.77	—

Energy partitioning

Ea = ΔEA + ΔEB + EAB

Procedure of energy partitioning by one-center and two-center components served qualitative rather than quantitative purposes. This is because in most cases no conclusion can be made as to reactivity judging by the value of stabilization energy EAB, because absolute values have reverse dependence: the higher is the activation barrier (i.e., the lower reactivity), the higher is the intermolecular interaction. In analysis, one must certainly consider deformational parts ΔEA and ΔEB in addition to interaction energy EAB. Analysis of EAB enabled us to reveal one more factor of substrate reactivity: coulomb interaction of electrophil and substituent. The point is that in TS this interaction significantly differs in sign and value from the initial one and disappears in σ-complex (due to charge neutralization of nitro group). Real reactivity may therefore differ from that predicted on either the base of structure of isolated reagents or the stability of products of reaction. For example, Table VIII demonstrates some characteristics obtained by energy partitioning analysis. Attention is drawn to certain evidence of this effect in reactions of phenylacetate and 2-biphenylcarbonic acid (X = -O-COCH3 and -Ph-COOH).

Table VIII. Activation energy (E_a) of NO2+ ortho attack, total energy of interaction of Ph-X and NO2 group (E_AB), its resonance component (E^res), component of coulomb interaction of NO2 group with substituent (E^q), and total charge of substituent in TS (Q_X).

−X	Ea, kcal/mol	EAB, eV	Eres, eV	Eq, eV	QX, e
* Charge of NO2 group in TSs ≈ 0.40 ÷ 0.45 e.
-CH3	0.1	−2.503	−2.386	0.268	0.157
-CF3	14.1	−3.202	−3.560	0.221	0.066
-C4H9, tret	−1.5	−2.326	−2.160	0.244	0.153
-NO2	18.2	−3.351	−3.748	−0.016	−0.026
-COOH	9.9	−3.228	−3.442	−0.032	0.017
-Cl	4.6	−2.679	−2.662	0.231	0.129
-O-COCH3	−6.3	−2.888	−2.547	−0.279	0.039
-Ph	−4.0	−2.748	−2.358	−0.004	0.247
-Ph-COOH, ortho	−6.9	−3.533	−3.389	−0.267	0.098

Perturbation molecular orbital theory, index of reactivity

Molecular orbitals of reagents obtained in gas-phase approximation were not suitable for PMO theory consideration, because E_HOMO (highest occupied molecular orbital) of arene and E_LUMO (lowest unoccupied molecular orbital) of nitronium (or nitracidium) are practically similar, −9 eV. This analysis was therefore performed on the basis of MOs determined in liquid-phase approximation where electronegativity of electrophils were much lower: E_LUMO ≈ −2 eV). Orbital interaction energy of PMO had unsatisfactory correlation with activation energies, proving that intermolecular interaction was not the only factor of reactivity. Introducing the parameter that describes coulomb interaction (Eq of Table VIII), gives two-variable linear correlation scheme. After that, coefficient of correlation increases from 0.82 to 0.94, but nevertheless such a scheme seems to be incorrect without account of deformation factor. Deformation energy may be evaluated by torsion of aromatic ring to some geometry. But let us consider another, more “natural” process: protonation of aromatic compound. All mentioned factors of reactivity join in enthalpy of protonation of aromatic substrates: deformation, orbital, and coulomb interaction. As shown in Figure 8, correlation is even better than that with enthalpy of original reaction itself (Fig. 6). The explanation lies in the fact that in σ-complex (product of addition) NO2 group has practically no electric charge, whereas in H+-complex there is considerable electrostatic interaction between electrophil (H+) and substituent, the same as that in TS of nitration reaction. It appears to be a nearly ideal index of reactivity for nitration, for it makes single correlation for ortho, meta, and para reactivity and satisfactorily covers ipso-attack and special cases of ortho peculiarities.

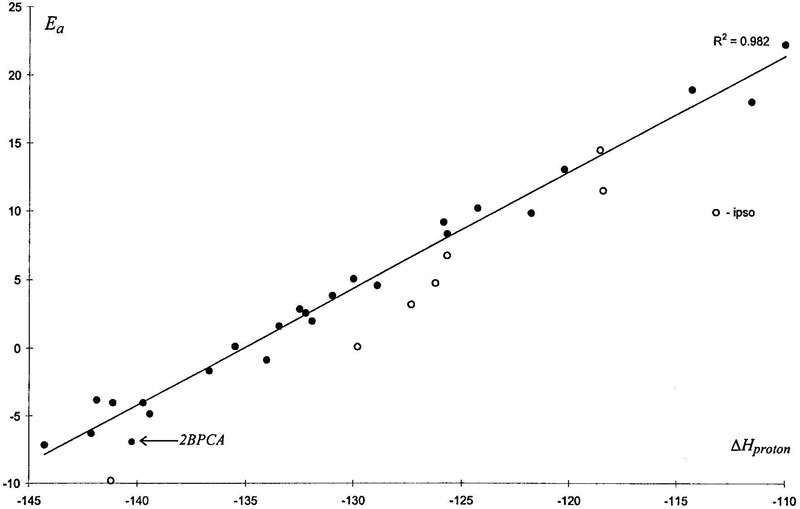Figure 8. Plot of activation energies of nitration versus enthalpy of protonation for AM1, gas phase, and kcal/mol (•, ortho, meta, and para; ○, ipso attack).

^* Increased reactivity of 2BPCA is an experimental fact, especially the high ortho/para ration of reaction products (from 3 to 8 depending on reaction conditions) [12].