Radical addition to the vinyl C=C bond: Quantum chemistry model of the reaction

Alternative Form of the PMO Equation: Effective Electronegativity of Reagent

Eq. (1) can be rewritten as

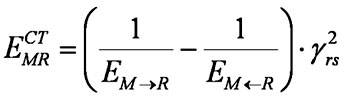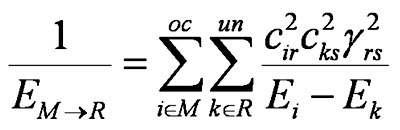(1') where and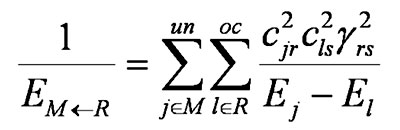

Values E_M→R and E_M←R may be considered efficient energies of occupied and unoccupied orbital shells of the first reagent M related to the orbitals of the second reagent R. A more convenient notation looks like this:

(2) where N = E_M→R + E_M←R and G = E_M←R − E_M→R.

Let us call parameter N by analogy with the Mulliken formula⁶ the efficient electronegativity (N) of reactive center (which describes acceptor/polar properties) and G the efficient energy gap between interacting orbital shells (which characterizes activity/sensitivity, covalent characters of interaction). As follows from the definition, parameters N and G are not characteristics of a whole reagent but of a certain reactive center. These parameters are useful in discussions concerning reactivity. For example, most simple vinyl monomers have similar values of G so their reactivity can be explained by N only. The dependence of CT energy upon N is of parabolic type with maximum at N = 0. That means that in the case when N of reagents coincide, stabilization via E^CT is the lowest. The group of monomers with conjugated double bonds (butadiene, styrene, vinylpyridene, etc.) were found to have close EN but strongly differed by energy gap between occupied and unoccupied orbital shells. In such a case, reactivity could be entirely explained by the factor G (see Table V). N is also convenient for discussions of electron donating and related polar effects. For example, EN satisfactorily correlates with charge transfer from monomers to the attacking radical.

Despite all this there is a great limitation of formula (2): parameters N/G are individual (relative) values for each reaction series, and so should be used in such a series with one fixed reagent. But such parameters of different series appeared to be linearly dependent! It cannot be true, but in some approximation it could happen for some narrow classes of reagents. Only a computational experiment can prove or deny it. And, it was revealed that ours was such a case. In all considered reactions, relative scales of monomers' N and G correlate linearly surprisingly well (see, e.g., Fig. 5). This makes it possible to build a sort of universal scale of N for the radical addition to vinyl C=C bond. So, Eq. (2) for CT energy obtain the following form, where gaps are summed and electronegatives are substracted:

(2')

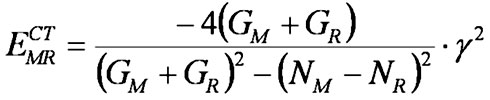
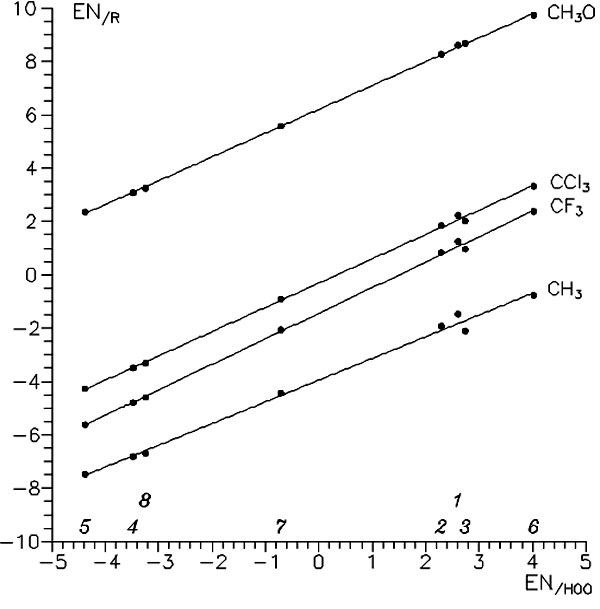Figure 5. Relation between effective electronegativities (parameters N) of vinyl monomers calculated for relatively different radicals. 1, Eth; 2, Prop; 3, St; 4, AN; 5, MA; 6, VA; 7, VCl; 8, VCl2.

The proposed procedure of calculation of N/G parameters has general character and by no means is restricted by frames of radical addition reaction or even π-approximation. Moreover, one can try to split total term on σ- and π-terms and so get two pairs of N/G parameters, one characterizing the σ shell and the other the π one.

⁶ Mulliken's definition of electronegativity: EN = ½ (E^HOMO + E^LUMO).