Radical addition to the vinyl C=C bond: Quantum chemistry model of the reaction

Results of the PMO Theory Approach

The PMO theory remains the best tool to discuss the reactivity of various chemical reactions. Our reaction is a suitable case for its application and, moreover, in π-approximation. The interaction energy of the PMO theory, also called «charge transfer» (CT) energy, has a well-known form:

(1)

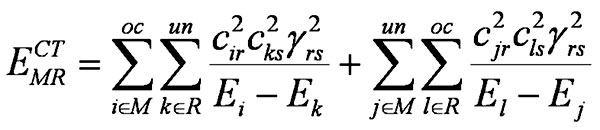
where summing is done over a set of spin orbitals and γ is the resonance integral on the atomic orbitals (AOs) of reactive centers r and s.

Using RHF π-orbitals of isolated reagents we calculated CT energies of all series in consideration (see, e.g., Tables V and VI). Figure 4 shows that there is some symbasis between them and the activation barriers of corresponding reactions. Addition to a substituted position gives less satisfactory correlations that are obviously caused by a greater steric effect (deformation of reaction center). So, E^CT could also be taken for another factor of reactivity. But, there is one inconvenience with it: It is not an ordinary index of reactivity; it is the whole set of energies of MOs and their coefficients of the AOs of the reaction center. It is no wonder that when using the PMO theory researchers frequently truncate orbital sets to HOMO and LUMO to avoid the summing in Eq. (1); this method is known as the frontier molecular orbitals (FMO) approach.

Although FMO cannot be approved as a true approximation ⁽⁵⁾ it has an obvious advantage: The coefficients and energies of FMO may be used as indices of reactivity. Another solution could be localized MOs. For example, using a projective procedure we managed to build a pair of localized MOs of a monomer that combined ≈95% of π-density both of occupied and unoccupied shells. It is a pity that even 5% is too great an error for such sums as Eq. (1). So, the wish appears to “adjust” energies (or coefficients) of such localized orbitals so that they would give exact values of the sums in Eq. (1). As a result, we would get some fictitious but effective orbitals. Now, we are going to propose an alternative notation of the PMO Eq. (1) that gives such effective MOs.

Table V. HOO• addition to vinyl monomers.

Monomer	β-attack				α-attack
	Ea	ECT	N	G	Ea	ECT	N	G
Ea, kcal/mol; ECT, (γ2/eV); N and G, in eV.
Eth	26.4	−0.286	1.304	14.1
Prop	25.8	−0.294	1.147	13.7	31.0	−0.285	1.460	14.2
AN	26.0	−0.287	−1.740	14.1	30.3	−0.271	0.284	14.8
MA	26.8	−0.284	−2.187	14.4	31.3	−0.270	0.726	14.8
VA	23.9	−0.307	2.011	13.3	26.8	−0.278	0.738	14.4
VCl	26.5	−0.284	−0.355	14.1	30.2	−0.273	0.233	14.7
VCl2	25.7	−0.289	−1.625	14.0	32.0	−0.266	−0.459	15.1
St	23.0	−0.311	1.371	13.0
ViNaph	22.7	−0.313	1.379	12.9
2ViPy	23.3	−0.303	0.788	13.3
4ViPy	23.4	−0.299	0.125	13.4
Bu2ene	22.6	−0.310	1.395	13.1
Hex3ene	21.8	−0.315	1.400	12.9

Table VI. CH3• addition to vinyl monomers.

Monomer	β-attack				α-attack
	Ea	ECT	N	G	Ea	ECT	N	G
Ea, kcal/mol; ECT, (γ2/eV); N and G, in eV.
Eth	13.9	−0.349	−0.735	11.5
Prop	13.6	−0.359	−0.960	11.2	18.1	−0.348	−0.675	11.5
St	11.4	−0.378	−1.054	10.7	−0.344	−0.766	11.7
AN	13.0	−0.391	−3.405	11.3	17.0	−0.355	−1.714	11.5
MA	13.4	−0.388	−3.738	11.5	18.0	−0.349	−1.342	11.6
VA	12.1	−0.370	−0.385	10.8	16.7	−0.346	−1.353	11.7
VCl	13.3	−0.369	−2.216	11.3	16.9	−0.354	−1.716	11.5
VCl2	12.6	−0.396	−3.343	11.1	19.6	−0.363	−2.394	11.5

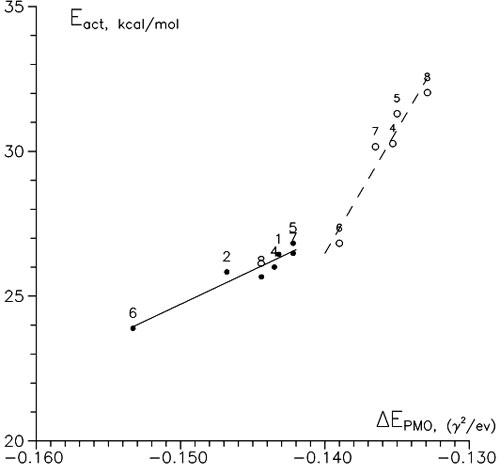Figure 4. Relationships between activation energies and CT energy of the PMO method, HOO addition. •, β-attack; ○, α-attack.