Radical addition to the vinyl C=C bond: Quantum chemistry model of the reaction

Energy Partitioning

Although we have obtained a powerful index of reactivity we remain uncertain of the factors that determine that reactivity. So, let us turn to energy partitioning and divide activation energies into their main parts: energies of former reagents, E^R and E^M, and interaction energies, E^int. Figure 2 shows the results of such partitioning. The whole situation seems to be complicated enough, each of those parts being greater in absolute value than the resulting activation energy, and no clear correlations are visible. Moreover, values of intermolecular interaction are antibate to activation energies, so they cannot be the main and only factor of reactivity. We can only mark some symbasis between barriers and deformation energies of monomers. As mentioned above, the deformation movement of vicinal substituents of the reaction center is the main part of the IRC at the TS point. So, we could expect a possible relationship between energies of a monomer's deformations (E^def) and activation energies. And, really, they appeared to correlate surprisingly well (Fig. 3).

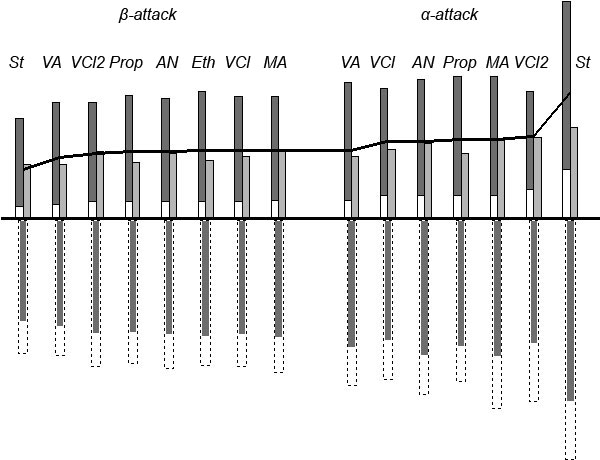Figure 2. Partitioning of activation energies of reactions HOO• + CH2CHX. 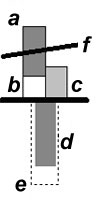Details of histogram: (a), E^M, the change of monomer's total energy including E^def, (b); (c), E^R, the change of total energy of HOO; (d), E^int, total energy of interaction; the dashed block (e) shows the value of interaction between reactive centers; (f), resulting value of activation barrier E_a (ΔΔH^≠_f).

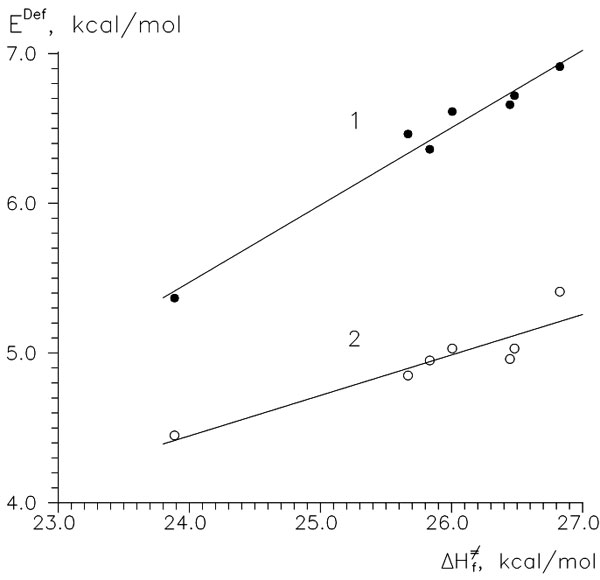Figure 3. Relationship between E_a of HOO β-addition and energies of deformation of vinyl monomers, kcal/M. 1—deformation to geometry of TS, 2—«standard» deformation E₀^def.

E_def cannot be a true parameter of reactivity – the degree of tortion directly depends on the distance between reagents in TS, which, in turn, depends on the reagents' reactivity itself. We need to adjust deformation to some standard conditions, for example, an average of considered geometries of TSs⁽³⁾. The values of such «standard» deformation energies (E₀^def) are shown in Table IV.

Table IV. Energies of standard deformation (E₀^def) of vinyl monomers (kcal/mol).

E0def	Eth	Prop	AN	MA	VA	VCl	VCl2	St
β-position	6.83	6.51	6.57	7.01	5.64	6.56	6.07	4.83
α-position		7.45	7.19	7.65	6.10	7.08	6.96	7.88

Figure 3 shows that there exists a close relationship between activation energy of addition and E₀^def of monomers. That means that vinyl monomers endure tortion with ease compared with their reactivity. All said, this does not suppose that reactivity is but an elastic property of a monomer because neither calculated force constants of valent C=C vibration nor umbrella CH2 vibration correlate with ΔΔH^≠_f ⁽⁴⁾. Moreover, it was found from other dependencies (other radicals' addition) that polar factors were also present: The monomers with acceptor group (VCl, MA, AN) had extra activity in reactions with CH3•; and vice versa, with CF3• or CH3O• they lacked some activity.

Thus, to discuss radical addition we need to consider two terms: intra- and intermolecular reforming. Let us choose E₀^def to represent the first factor. Then the second, intermolecular term, can be described by means of the PMO theory. And, our case is a good one for π-approximation.

⁽³⁾ The following average geometry was taken for standard: valence angle 119°, torsion angle of vicinal CH bonds −15°, and C=C bond lengthening 4.8%.

⁽⁴⁾ Calculated force constants of valent C=C vibration of monomers (N/cm): St, 12.6; VA, 12.6; Prop, 12.8; VCl2, 12.2; AN, 12.6; Eth, 13.0; VCl, 12.8; MA, 12.7.