Radical addition to the vinyl C=C bond: Quantum chemistry model of the reaction

Empirical Schemes of Vinyl Monomers' Relative Reactivity in Radical Addition Reactions

In the previous paragraph we proposed to try Eq. (3), or just its polar part, as a basis of nonlinear empirical schemes of reactivity. This approach is intended for calculation or prediction of rate constants (or activation barriers) in cases when the differences in the structure of reagents are too great to use linear correlation schemes of the Hammett type. Let us try to build a scheme of reactivity of vinyl monomers in radical addition reactions. Firstly, we can use only the form of Eq. (3), its parameters being the variables for the optimization procedure. On the other hand, we can try to use theoretically obtained parameters of vinyl monomers as indices of reactivity and correlate experimental data with them.

Both variants were studied. Let's start from entirely empirical method, the first approach. For this purpose we are going to use a slightly simplified form of Eq. (3) (supposing only EN influences the value of CT energy⁽⁷⁾ ):

(4)

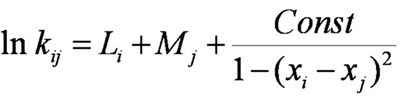
where L_i and x_i are parameters of a radical and M_j and x_j of a monomer (x is the EN of a reagent; L and M collect entropy, nonpolar effects, and so on). Because only relative rate constants of radical addition to monomers were considered (ln k_ij/k_ik), parameter L never appeared. Parameterization of the scheme was accomplished on the basis of approximately 200 rate constants [1, 7, 9] of reactions between 20 chosen radicals and 20 vinyl monomers. All obtained parameters are shown in Table IX (see more data in Ref. [10]). Comparison of calculated values with experimental data are shown in Figure 7. It enables us to say that the proposed scheme describes these experimental data reasonably well (mean deviation is less than 50%, the precision of those kinetic data themselves). So, the form of Eq. (4) is both meaningful and adequate for the purposes of nonlinear correlation tasks. It is relevant to add here that all parameters also “correlate” with common chemical views on donor–acceptor properties of both the radicals and monomers that were considered.

Table IX. Optimized parameters of reagents, Eq. (4). Const = 27.5

Monomer	M	x	Radical	x
* Styrene parameters were used as reper values. ** Additional abbreviations of vinyl monomers: MSt, α-methylstyrene; MAN, methacrylic nitryl; MMA, methyl methacrylate; IPA, isopropenylacetate; VBuE, vinyl buthyl ether; ViPy, vinylpyridine; MVK, methylvinylketone; DPE, diphenylethene; VF, vinyl fluoride. *** Polyalkyl radicals ∼CH2−C•HY, generated from vinyl monomers in polymerization.
St	0*	0	CH3•	0.477
MSt**	0.284	0.0081	t-Bu	0.518
AN	−1.908	−0.0559	c-C6H11•	0.587
MAN	−1.585	−0.0218	5-C6H9•	0.528
MA	−2.085	−0.0482	C6H5•	0.310
MMA	−1.006	−0.0315	C6H5-S•	−0.534
VA	−4.582	−0.0285	t-BuO•	−0.482
IPA	−4.061	−0.0149	t-BuOO•	−0.541
VBuE	−5.200	0.0102	PhC(CH3)2OO•	−0.372
2-ViPy	0.251	−0.0122	CCl3•	−0.204
4-ViPy	−0.023	−0.0114	CF3•	−0.627
1,1-DPE	1.216	0.0122
1,2-DPE	−1.660	0.0093	poly-St***	0.446
VCl	−3.034	−0.0253	poly-MSt	0.598
VCl2	−2.097	−0.0449	poly-AN	−0.293
VF	−5.087	−0.0219	poly-MAN	0.072
VF2	−3.522	−0.0604	poly-MA	0.157
Eth	−4.431	−0.0167	poly-MMA	0.088
MVK	−1.729	−0.0561	poly-VA	0.067

There are experimental data on reactivity of radicals and vinyl monomers that have substituted benzoic ring in theirs structure. In the process of parametrization we assumed that substituent in such aromatic compounds only shifts EN of the reagent: x_i=x₀ + ρ σ_i, where ρ is the sensitivity quotient and σ_i is parameter of substituent (they correspond both by the meaning and value the Hammett's ρ/σ parameters [2]); see Table X.

Table X. Parameters^* of substituents (σ) in aromatic ring. Sensibility of aromatic groups for substitution (ρ).

substituent	σ**	group	ρ
*gained by optimization procedure; **σH = 0; ***ρPhS = 1 was set as the reper value
p-NH2	0.111	Ph-S •	1.0***
p-OCH3	0.042	Ph­CH=CH2	0.145
p-CH3	0.004	Ph­CH •∼	0.936
p-Cl	−0.013	Ph•	2.4
p-Br	−0.009
p-CN	−0.030
p-NO2	−0.041

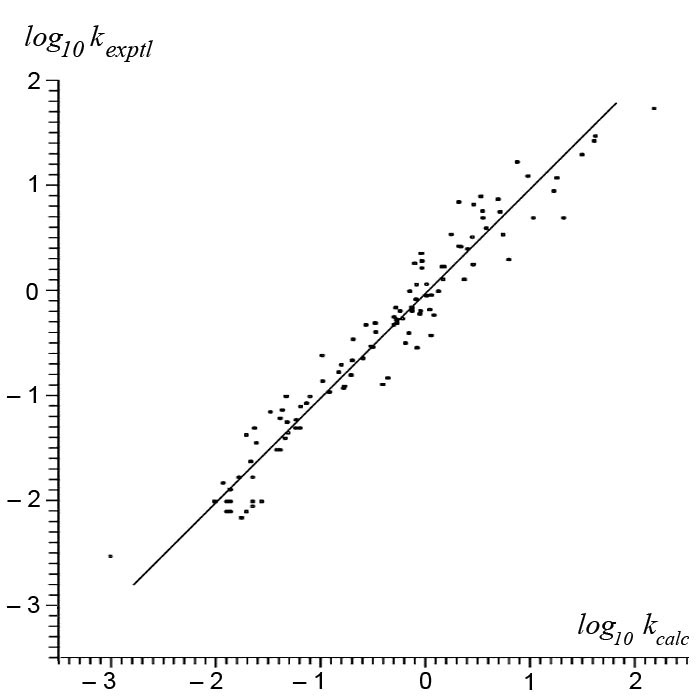Figure 7. Relationship between experimental relative rate constants and calculated values [Eq. (4)]

Try Online Calculator

Another method of utilizing Eq. (3) is using its polar part as a theoretical index of reactivity. So, we are going to tabulate electronegativities and energy gaps of monomers and use them as parameters of activity for correlation purposes. This time only linear (M_j) parameters of monomers shall be obtained through optimization. The working equation of such a scheme be

(5)

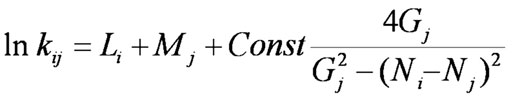
The set of optimized parameters M_j is presented in Table XI. The quality of prediction of this scheme is a bit lower than that of the previous one (mean deviation of calculated rate constants is approximately 60%). But, it has the considerable advantage of being “semiempirical” because the number of empirical parameters is essentially reduced and an important part of predictions is based on values calculated by quantum chemistry.

Table XI. Parameters of the “semiempirical” scheme, Eq. (5)]. Const = 80 (optimized value).

Monomer	M	N	G	Radical	N
Parameters N/G of monomers calculated with relatively HOO• were used. Parameters N of radicals were obtained by optimization procedure, while G of different reaction series were supposed to be equal.
St	0.00	1.37	13.0	CH3•	1.26
MSt	−0.45	1.19	12.8	c-C6H11•	2.75
AN	0.78	−1.74	14.1	5-C6H9•	3.42
MAN	1.05	−1.69	13.8	t-Bu•	2.52
MA	0.76	−2.19	14.4	t-BuO•	−2.71
MMA	1.39	−2.08	14.0	t-BuOO•	−2.74
VA	−4.42	2.01	13.3	PhC(CH3)2OO•	−2.36
IPA	−5.50	2.00	13.0	Cl-PhS•	−2.73
Eth	−2.04	1.30	14.1	CF3	−4.00
VBuE	−6.34	3.19	13.2	CCl3	−0.70
VCl	−0.73	−0.36	14.1	poly-IPA	−0.76
VCl2	0.55	−1.63	14.0	poly-VA	−0.82
2ViPy	0.80	0.79	13.3	poly-MMA	−1.03
4ViPy	0.87	0.13	13.4	poly-MA	−0.52
MVK	0.86	−1.46	14.2	poly-MAN	−1.43
1,1-DPE	2.86	0.80	13.6	poly-AN	−2.09
VF	−3.28	1.00	13.7	poly-MSt	2.73
				poly-St	1.86

⁽⁷⁾ The parameter corresponding to the energy gap of reagents is absent in this scheme because it has been found that it may be set constant (variation of such an expanded form of equation gave no improvement).