Radical addition to the vinyl C=C bond: Quantum chemistry model of the reaction

Comparison of Direct TS Calculations with Indices of Reactivity

Let us return to our consideration of radical addition. Earlier, we suggested that the activation energy of this reaction is a total of two effects: deformation and polar interaction. The first can be evaluated by standard deformation energy, E₀^def (see above), and the second by CT energy of the PMO method. To try the possibility of a general scheme of radical activity, all previously obtained results of direct TS calculations were considered within the following equation:
(3) E_a = a₀ + a₁E₀^def + a₂E^CT

To use the advantages of the N/G method of calculation of E^CT we used the formula (2')

Parameters N and G calculated relatively HOO• were used for the standard set of monomers' parameters. Parameters of radicals could be easily derived from linear dependencies shown in Figure 5. So, we just needed to obtain parameters a₀, a₁, a₂ of reactions. That was done by the usual optimization procedure. But, it was found that parameters of radicals obtained from π-approximation poorly correspond to the true picture of reactivity (and, really, they have considerable σ-character in TS). So, we decided to adjust parameters of radicals within the same optimization process. Final optimized values are collected in Tables VII and VIII. Figure 6 shows the quality of usage of Eq. (3) for evaluation of activation energies.

Table VII. Parameters of vinyl monomers; see Eq. (3)

	β-addition			α-addition
	Edef	N	G	Edef	N	G
Edef, kcal/mol; N, G, eV
Eth	6.83	1.30	14.1
Prop	6.51	1.15	13.7	7.45	1.46	14.2
AN	6.57	−1.74	14.1	7.19	0.28	14.8
MA	7.01	−2.19	14.4	7.65	0.73	14.8
VA	5.64	2.01	13.3	6.10	0.74	14.4
VCl	6.56	−0.36	14.1	7.08	0.23	14.7
VCl2	6.07	−1.63	14.0	6.96	−0.46	15.1
St	4.82	1.37	13.0	7.88	1.40	14.3
Bu2	4.786	1.39	13.1
Hex3	4.438	1.40	12.9
ViNaph	4.890	1.38	12.9
2ViPy	5.204	0.79	13.3
4ViPy	5.113	0.12	13.4
4ViPm	5.611	−0.42	13.6
2ViPm	5.783	−0.32	13.4

Table VIII. Optimized^* parameters of radicals and their reaction series. N, G in eV. Optimized scaling factor a₂ = 40 [see Eq. (3)].

	N	G	β-addition		α-addition
			a0	a1	a0	a1
* HOO is chosen to be the reper reactant, so relative parameters of other radicals are presented here (N < 0 means a more electronegative and G < 0 a more “sensitive” radical).
HOO	0	0	28.0	1.46	20.8	2.85
CH3	1.60	−1.00	21.0	0.75	23.8	0.75
CH3O	−0.55	−0.65	26.2	0.92	14.0	3.05
CCl3	−1.75	−1.30	28.6	0.80	24.3	2.00
CF3	−3.50	−0.23	23.8	0.60	16.0	2.30

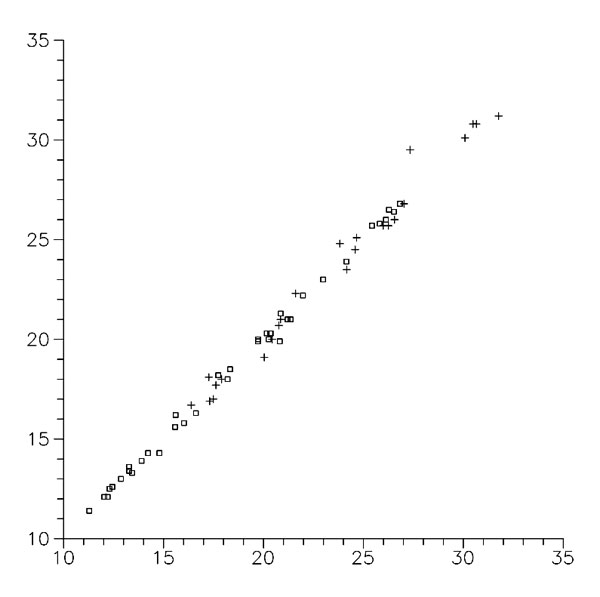Figure 6. Relationship between directly calculated activation energies and those evaluated by Eq. (3) values, kcal/M (β-addition indicated by □, α-addition by +).

The main significance of that correlation is that regulations of radical addition to the C=C bond (how they are seen by semiempirical methods of quantum chemistry) could be explained by the electronic structure of reagents using two indices of reactivity: ability of reaction center to deform and change its hybridization and the energy of interaction of π-MOs of reagents. It is a justification of our next step: to explain experimental regulations by these same characteristics of reagents and try the mathematical form of Eq. (3) for a correlation analysis of experimental data.