Реакционная способность в реакциях радикального присоединения к ненасыщенным соединениям

Альтернативная форма уравнения ВМО. Эффективная электроотрицательность

Выражение (1) можно переписать так:

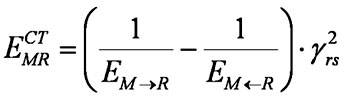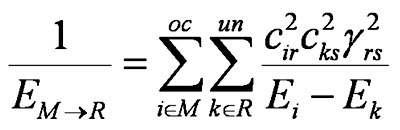(1') где and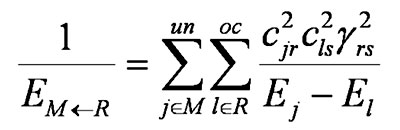

Значения E_M→R и E_M←R можно интерпретировать как эффективные энергии занятой и свободной орбитальных оболочек первого реагента M в отношении к орбиталям второго реагента R. Более удобная запись выглядит так:

(2) где N = E_M→R + E_M←R and G = E_M←R − E_M→R.

Назовем параметр N по аналогии с формулой Малликена⁶ эффективной электроотрицательностью реакционного центра (он описывает акцепторные/полярные свойства), а G – эффективной энергетической щелью между взаимодействующими орбитальными оболочками (он характеризует активность/чувствительность реакционного центра, ковалентный характер взаимодействия). Как следует из определения, параметры N и G не являются характеристиками реагента в целом, а его определенного реакционного центра. Эти параметры удобны для обсуждения реакционной способности. Например, бóльшая часть винильных мономеров имеют близкие значения G, поэтому их реакционная способность может быть объяснена значением N, их электроотрицательности. Зависимость E^CT от N носит параболический характер с максимумом в точке N = 0. Это означает, что в случае, когда электроотрицательности реагентов совпадают, стабилизация за счет E^CT минимальна. Наоборот, было найдено, что группа мономеров с сопряженными двойными связями (бутадиен, стирол, винилпиридин и т.д.) имеют близкие N, но сильно различаются значением G, энергетической щелью между своими занятыми и свободными электронными оболочками. В этом случае реакционная способность может быть объяснена величиной G мономера (см. Таблицу V). N также удобен для обсуждения донорно-акцепторных свойств реакционных центров реагентов. К примеру, N удовлетворительно коррелирует с переносом электронной плотности с мономера на атакующий радикал.

Несмотря на все эти удобства, формула (2) имеет существенное ограничение: параметры N/G есть индивидуальные (относительные) значения для каждой реакционной серии, т. е. должны быть использованы лишь в серии реакций с фиксированным реагентом. К счастью оказалось, что параметры разных реакционных серий практически линейно зависимы. В общем случае такого не должно быть, но в выделенном узком классе реакций такое приближение возможно. Таковым оказался рассматриваемый нами класс реакций: вычислительный эксперимент показывает, что во всех рассмотренных нами реакционных сериях шкалы параметров N и G удивительно хорошо коррелируют! (см., например, Рис. 5). Это делает возможным построение некоторой универсальной шкалы электроотрицательностей для реакции радикального присоединения к винильной C=C связи. Так что выражение (2) для E^CT принимает следующий форму, где энергетические щели реагентов суммируются, а электроотрицательности вычитаются:

(2')

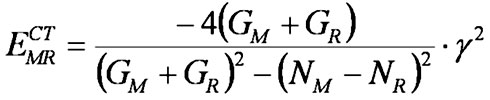
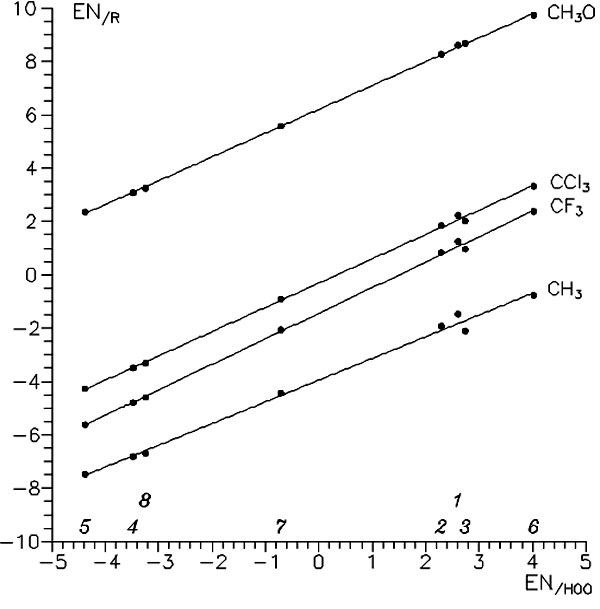Рисунок 5. Соотношение между эффективными электроотрицательностями (параметры N) винильных мономеров, рассчитанных относительно разных радикалов. 1, Eth; 2, Prop; 3, St; 4, AN; 5, MA; 6, VA; 7, VCl; 8, VCl2.

Предложенная здесь процедура расчета N/G параметров носит общий характер, и никоим образом не ограничивается рамками реакции радикального присоединения или даже π-приближением. Можно разделить общую сумму на σ- and π-части и получить две пары N/G параметров; одна будет характеризовать σ оболочку, а другая – π .

⁶ Малликеновское [Mulliken] определение электроотрицательности: EN = ½ (E^HOMO + E^LUMO).