Реакционная способность в реакциях радикального присоединения к ненасыщенным соединениям
Сравнение результатов прямых расчетов ПС с ИРС
Вернемся к нашему рассмотрению реакционной способности винильных мономеров.
Ранее мы предположили, что энергия активации складывается из двух частей: деформационная составляющая и энергия межмолекулярного взаимодействия. Первую можно количественно охарактеризовать с помощью энергии "стандартной" деформации E0def (см. выше), а вторую – с помощью теории ВМО величиной ECT. Для проверки такого предположения все ранее полученные результаты прямых расчетов ПС были обработаны в рамках следующей двухпараметровой корреляционной схемы:
(3)
Ea = a0 + a1E0def + a2ECT
Или, используя преимущества N/G метода расчета ECT мы использовали форму (2')
![]()
Параметры N and G, рассчитанные относительно HOO•, были использованы в качестве стандартного набора параметров мономеров. Параметры радикалов могут быть легко выведены из линейных зависимостей, представленных на Рис. 5. Так что нам необходимо найти a0, a1, a2 для рассматриваемых реакций. Такая оптимизация была выполнена методом наименьших квадратов. Однако обнаружилось, что параметры радикалов от
π-приближения плохо передают реакционную способность радикалов, имеющих во многом σ-характер в ПС.
Поэтому было решено скорректировать параметры радикалов той же оптимизационной процедурой. Результирующие оптимальные величины представлены в Таблицах VII и VIII. Рисунок 6 демонстрирует качество выражения (3) для оценки энергий активации.
| β-addition | α-addition | |||||
|---|---|---|---|---|---|---|
| Edef | N | G | Edef | N | G | |
| Edef, ккал/моль; N, G, эВ | ||||||
| Eth | 6.83 | 1.30 | 14.1 | |||
| Prop | 6.51 | 1.15 | 13.7 | 7.45 | 1.46 | 14.2 |
| AN | 6.57 | −1.74 | 14.1 | 7.19 | 0.28 | 14.8 |
| MA | 7.01 | −2.19 | 14.4 | 7.65 | 0.73 | 14.8 |
| VA | 5.64 | 2.01 | 13.3 | 6.10 | 0.74 | 14.4 |
| VCl | 6.56 | −0.36 | 14.1 | 7.08 | 0.23 | 14.7 |
| VCl2 | 6.07 | −1.63 | 14.0 | 6.96 | −0.46 | 15.1 |
| St | 4.82 | 1.37 | 13.0 | 7.88 | 1.40 | 14.3 |
| Bu2 | 4.786 | 1.39 | 13.1 | |||
| Hex3 | 4.438 | 1.40 | 12.9 | |||
| ViNaph | 4.890 | 1.38 | 12.9 | |||
| 2ViPy | 5.204 | 0.79 | 13.3 | |||
| 4ViPy | 5.113 | 0.12 | 13.4 | |||
| 4ViPm | 5.611 | −0.42 | 13.6 | |||
| 2ViPm | 5.783 | −0.32 | 13.4 | |||
| N | G | β-addition | α-addition | |||
|---|---|---|---|---|---|---|
| a0 | a1 | a0 | a1 | |||
* HOO выбран в качестве реперного реагента, так что здесь представлены относительные параметры остальных радикалов (N < 0 означает бóльшую электроотрицательность, G < 0 – бóльшую “чувствительность” радикала). | ||||||
HOO | 0 | 0 | 28.0 | 1.46 | 20.8 | 2.85 |
CH3 | 1.60 | −1.00 | 21.0 | 0.75 | 23.8 | 0.75 |
CH3O | −0.55 | −0.65 | 26.2 | 0.92 | 14.0 | 3.05 |
CCl3 | −1.75 | −1.30 | 28.6 | 0.80 | 24.3 | 2.00 |
CF3 | −3.50 | −0.23 | 23.8 | 0.60 | 16.0 | 2.30 |
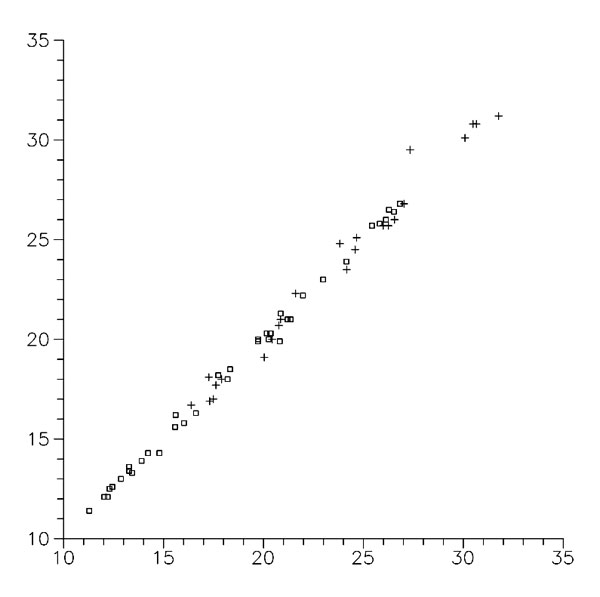 Рисунок 6. Соотношение между величинами прямых расчетов энергий активации и значениями, полученными в результате оценки по выражению (3), ккал/моль (□, β-присоединение; +, α-присоединение).
Рисунок 6. Соотношение между величинами прямых расчетов энергий активации и значениями, полученными в результате оценки по выражению (3), ккал/моль (□, β-присоединение; +, α-присоединение).
Важность полученной здесь корреляции заключается в том, что закономерности реакционной способности в радикальном присоединении к C=C связи (так, как они видятся полуэмпирическим методам расчета) могут быть количественно объяснены исходя из электронного строения реагентов, при использовании двух индексов реакционной способности: способности реакционного центра к деформации и энергии взаимодействия π-орбиталей реагентов. Она является обоснованием нашего следующего шага:
объяснения экспериментальных закономерностей теми же характеристиками реагентов и попытки использования математической формы выражения (3) для корреляционного анализа экспериментальных данных.
