Реакционная способность в реакциях радикального присоединения к ненасыщенным соединениям
Процедура разделения энергии
Хотя мы получили индекс реакционной способности (ИРС), мы пока остаемся в неведении относительно факторов, которые определяют эту реакционную способность. Воспользуемся процедурой разделения энергии (energy partitioning), и разобьем энергию активации на ее основные составляющие: энергии "реагентов", ER и EM, и энергию взаимодействия между ними, Eint. На Рисунке 2 представлены результаты такой процедуры. Ситуация в целом кажется довольно сложной: каждая из превышает (по абсолютному значению) величину самого барьера активации, и не наблюдается никакой особой зависимости. Более того, значения энергии межмолекулярного взаимодействия антибатны энергиям активации; следовательно не могут быть единственным или основным фактором реакционной способности. Ранее отмечалось, что деформационное движение вицинальных заместителей при реакционном центре является основной составляющей координаты реакции (IRC) на момент переходного состояния, поэтому мы могли бы ожидать взаимосвязь энергии деформации мономера и активационного барьера. Процедура разделения энергии дает лишь энергию "молекулы реагента" в составе супермолекулы, энергию не только деформации, но и электронной перестройки. Будем называть энергией деформации энергию изменения геометрии молекулы к той, что она имеет в переходном состоянии. Расчет таких величин (Edef) показывает, что они действительно коррелируют неплохо коррелируют с барьером активации (см. Рис. 3).
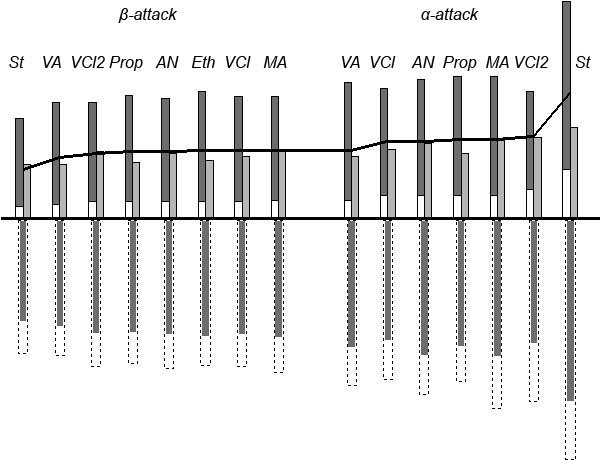 Рисунок 2. Результат процедуры разделения энергии активацииреакции
Рисунок 2. Результат процедуры разделения энергии активацииреакции HOO• + CH2CHX.
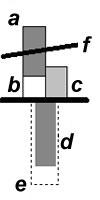 Детали гистограммы:
(a) EM, изменение общей энергии мономера, включая энергию деформаци (b) Edef (см. текст); (c) ER, изменение общей энергии радикала
Детали гистограммы:
(a) EM, изменение общей энергии мономера, включая энергию деформаци (b) Edef (см. текст); (c) ER, изменение общей энергии радикала HOO; (d) Eint, общая энергия межмолекулярного взаимодействия; пунктиром (e) показан вклад взаимодействия реакционных центров; (f) результирующая величина энергии активации Ea (ΔΔH≠f).
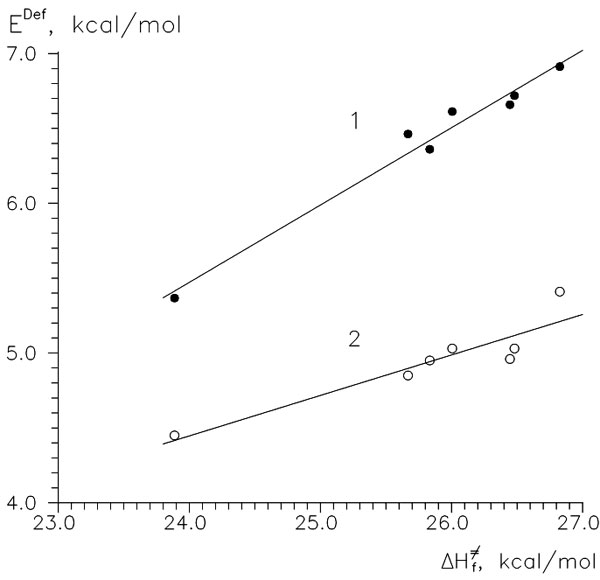 Рисунок 3. Взаимосвязь Ea реакции
Рисунок 3. Взаимосвязь Ea реакции HOO β-присоединения и энергий деформации винильных мономеров, ккал/моль. 1—деформация к геометрии ПС, 2—"стандартная" деформацияE0def.
Edef не может служить подходящим ИРС – степень деформации мономера зависит от расстояния между реагентами в ПС, которое, в свою очередь, зависит от реакционной способности мономера. Для расчета ИРС мономеров следует ввести некоторую единую величину деформации. Например, нечто среднее для данного класса реакций(3). Величины такой "стандартной" деформации (E0def) собраны в Таблице IV.
| E0def | Eth | Prop | AN | MA | VA | VCl | VCl2 | St |
|---|---|---|---|---|---|---|---|---|
| β-положение | 6.83 | 6.51 | 6.57 | 7.01 | 5.64 | 6.56 | 6.07 | 4.83 |
| α-положение | 7.45 | 7.19 | 7.65 | 6.10 | 7.08 | 6.96 | 7.88 |
Рисунок 3 показывает, что есть тесная связь между энергией активации и E0def мономеров. Это означает, что винильные мономеры поддаются деформации соответственно их реакционной способности. Однако это не означает, что РС мономеров определяется лишь упругими свойствами его C=C связи: ни расчетная силовая постоянная валентного C=C колебания, ни зонтичного CH2 колебания не коррелирует с ΔΔH≠f (4). Более того, при анализе таких корреляций для других радикалов обнаруживается, что полярный эффект тоже присутствует: мономеры с акцепторными группами (VCl, MA, AN) имеют повышенное сродство с CH3•; и, наоборот, с CF3• или CH3O• они менее активны.
Таким образом, полное описание реакции радикального присоединения требует одновременного учета двух слагаемых: энергий внутри- и межмолекулярной перестройки. Возьмем в качестве меры первого фактора E0def, а межмолекулярное взаимодействие попробуем описать средствами теории ВМО, тем более, что к нашему случаю подойдет π-приближение.
(3) Следующая усредненная геометрия ПС была выбрана за "стандарт" для расчета E0def: валентный угол 119°, торсионный угол вицинальных CH связей −15°, удлинение C=C связи 4.8%.
(4) Расчетные силовые постоянные валентного колебания C=C связи мономеров (Н/см): St, 12.6; VA, 12.6; Prop, 12.8; VCl2, 12.2; AN, 12.6; Eth, 13.0; VCl, 12.8; MA, 12.7.
