Реакционная способность в реакциях радикального присоединения к ненасыщенным соединениям

Рассмотрение реакции с помощью теории ВМО

Теория ВМО по-прежнему является главным инструментом при рассмотрении реакционной способности различных химических реакций. Наш случай хорош тем, что можно ограничиться π-приближением.

Энергия межмолекулярного взаимодействия, исторически также именуемая энергией переноса заряда (CT, charge transfer energy), в теории ВМО дается известным выражением:

(1)

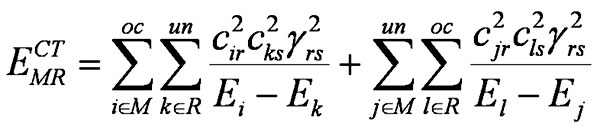
где суммирование выполняется по набору спин-орбиталей, а γ – резонансный интеграл на атомных орбиталях реакционных центров r и s.

Используя ОХФ π-орбитали изолированных реагентов мы рассчитали E^CT для всех рассматриваемых реакционных серий (см., например, Таблицы V и VI). Рисунок 4 демонстрирует существование некоторого соответствия между E^CT и энергиями активации соответствующих реакций. Присоединение к замещенной позиции двойной связи (α-присоединение) дает менее удовлетворительную зависимость, что, очевидно, связано с бóльшим стерическим эффектом (энергией деформации реакционного центра).

Итак, будем использовать E^CT в качестве второго фактора реакционной способности. Есть лишь одно неудобство: это необычный ИРС (приписывемый конкретной молекуле), а величина, сложным образом зависящая от электронного строения МО обоих реагентов (см. выражение 1). Поэтому неудивительно, что при использовании ВМО многие стремятся "урезать" набор МО реагентов, оставив только высшую занятую (HOMO) и низшую свободную (LUMO) молекулярные орбитали для того, чтобы избежать суммирования в выражении (1); этот подход известен как приближение граничных орбиталей (ГО).

Хотя приближение ГО не может быть признано удовлетворительным приближением для теории ВМО⁽⁵⁾, оно имеет явное практическое преимущество: наборы коэффициентов и энергий ГО можно использовать в качестве индексов реакционной способности! Альтернативой могли бы послужить локализованные молекулярные орбитали (например, используя процедуру проективной локализации можно построить пару локализованных π-орбиталей мономера, которая включает ≈95% общей π-плотности. К сожалению, даже 5% слишком большая погрешность для суммы (1). Так что появляется желание подправить энергии и коэффициенты "действительных" МО, чтобы получить некие фиктивные, "эффективные" орбитали. Эффективные в том смысле, что они будут точно воспроизводить результат суммирования (1). Так что сейчас мы перепишем уравнение теории ВМО (1) в удобном для нас виде и получим такие эффективные МО.

Таблица V. Присоединение HOO• к винильным мономерам.

Мономер	β-атака				α-атака
	Ea	ECT	N	G	Ea	ECT	N	G
Ea, kcal/mol; ECT, (γ2/эВ); N и G, эВ.
Eth	26.4	−0.286	1.304	14.1
Prop	25.8	−0.294	1.147	13.7	31.0	−0.285	1.460	14.2
AN	26.0	−0.287	−1.740	14.1	30.3	−0.271	0.284	14.8
MA	26.8	−0.284	−2.187	14.4	31.3	−0.270	0.726	14.8
VA	23.9	−0.307	2.011	13.3	26.8	−0.278	0.738	14.4
VCl	26.5	−0.284	−0.355	14.1	30.2	−0.273	0.233	14.7
VCl2	25.7	−0.289	−1.625	14.0	32.0	−0.266	−0.459	15.1
St	23.0	−0.311	1.371	13.0
ViNaph	22.7	−0.313	1.379	12.9
2ViPy	23.3	−0.303	0.788	13.3
4ViPy	23.4	−0.299	0.125	13.4
Bu2ene	22.6	−0.310	1.395	13.1
Hex3ene	21.8	−0.315	1.400	12.9

Таблица VI. Присоединение CH3• к винильным мономерам.

Мономер	β-атака				α- атака
	Ea	ECT	N	G	Ea	ECT	N	G
Ea, kcal/mol; ECT, (γ2/эВ); N и G, эВ.
Eth	13.9	−0.349	−0.735	11.5
Prop	13.6	−0.359	−0.960	11.2	18.1	−0.348	−0.675	11.5
St	11.4	−0.378	−1.054	10.7	−0.344	−0.766	11.7
AN	13.0	−0.391	−3.405	11.3	17.0	−0.355	−1.714	11.5
MA	13.4	−0.388	−3.738	11.5	18.0	−0.349	−1.342	11.6
VA	12.1	−0.370	−0.385	10.8	16.7	−0.346	−1.353	11.7
VCl	13.3	−0.369	−2.216	11.3	16.9	−0.354	−1.716	11.5
VCl2	12.6	−0.396	−3.343	11.1	19.6	−0.363	−2.394	11.5

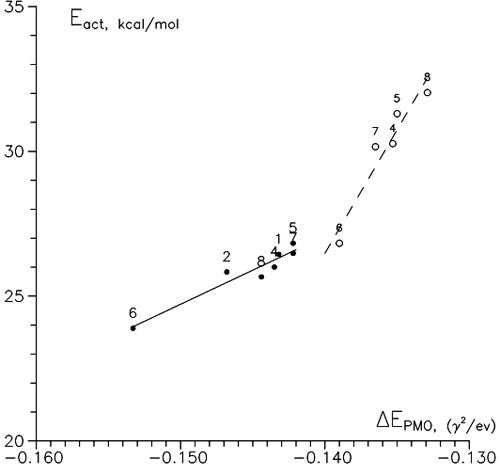Рисунок 4. зависимость между энергиями активации и энергиями переноса заряда метода ВМО, HOO присоединение. • – β-атака; ○ – α-атака.